
解法一
关于这个我在网上找到了答案,常见的解法如下:
1 | var x = (e.pageX - this.offsetLeft - (w / 2)) * (w > h ? (h / w) : 1); |
解题思路:
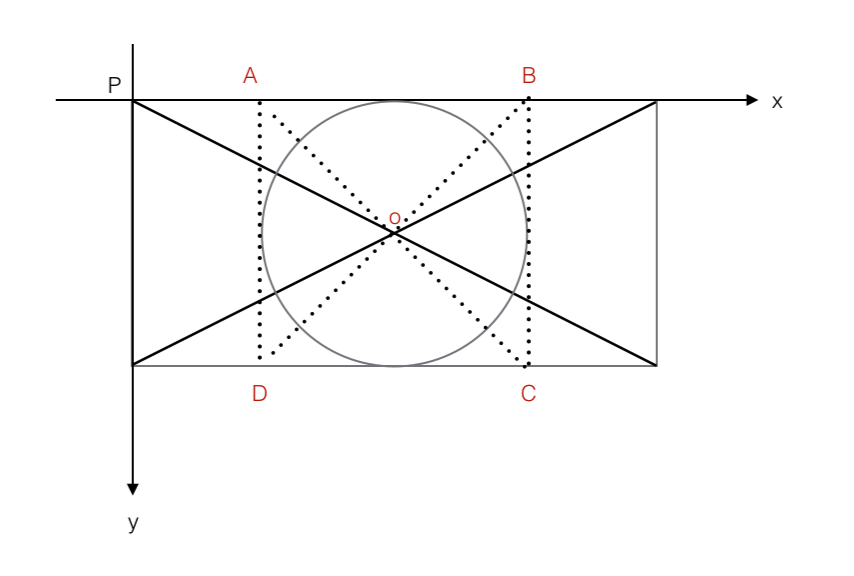
1、主要是将这个问题化为角度来算;
2、我们将P设为原点(this.offetLeft, this.offetTop),o设为圆心(this.offsetLeft + (w / 2), this.offsetTop + (h / 2));
3、鼠标移入该容器相对于圆心o的坐标为(e.pageX - o.x, e.pageY - o.y),即上文的(e.pageX - this.offsetLeft - (w / 2))与(e.pageY - this.offsetTop - (h / 2));
4、(w > h ? (h / w) : 1)与(h > w ? (w / h) : 1)的意思就是将矩形换算为正方形,例如有一个宽3x,高是x的矩形,相对原点P的右下角坐标就是{x:3x,y:1x},换算成正方形,即坐标点为正方形的右下角,矩形的四个角即一一对一个正方形的四个角形成正方形ABCD;
5、Math.atan2(x, y)返回角度值,换算成弧度则为((Math.atan2(y, x) * (180 / Math.PI)),结果为(-180, 180),加上180,就是(0, 360)。
6、除以90,即跟4一样道理,AoD,DoC,CoB,BoA都是90度角,目的就是将矩阵的角度跟方形的角度做个换算。
7、加3是因为想让计算的顺序为上,之前我们的角度区间是从右边开始,那么加3就会从上开始计算,也就是上,右,下,左的顺序;
8、Math.round以及4取模使得计算结果为0,1,2,3,为什么要这么做呢?Math.round使得坐标轴45度角划分四个象限,而4取模就可以知道鼠标移入移出是在计算过后的哪个象限了。
解法二
根据斜率,转自http://www.cnblogs.com/lyzg/p/5689761.html
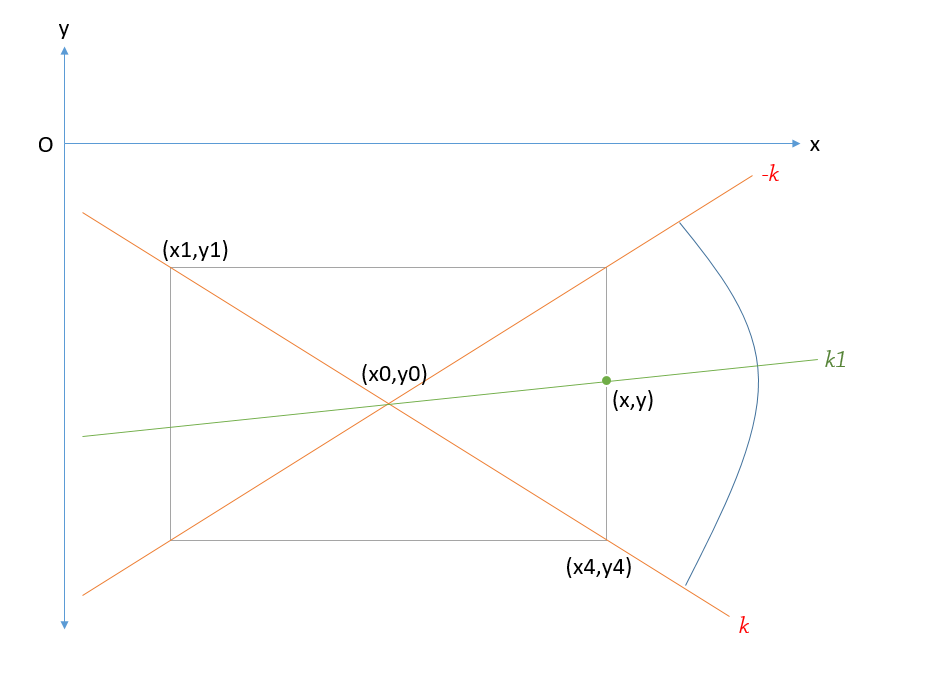
1、上图以浏览器可视区域左上角为原点建立坐标系,坐标系与数学坐标系方向一致,往右表示x轴正方向,往下表示y轴负方向;
2、图中点(x1,y1)代表元素框左上角,(x4,y4)代表元素框右下角,(x0,y0)代表元素框的中心点,(x,y)表示鼠标移入移出时与元素框的边的交点;
3、根据下面的公式:(y2 - y1) / (x2 - x1)
可得(x1,y1)与(x4,y4)这条对角线的斜率为 k = (y1-y4)/(x1-x4)。由于对称性,元素框另外一条对角线的斜率一定是 -k。
同时由于(x1,y1)与(x4,y4)这条对角线在坐标系中一定经过的是第二和第四象限,所以k肯定是负值,而 -k一定是正值。
4、根据同样的公式,当鼠标移入移出时的瞬间,与元素边框的交点与元素框中心点的斜率 k1 = (y-y0)/(x-x0)。
5、由图可知,当 k < k1 < –k时,鼠标一定是从元素的左右方向移动的;反之,一定是从上下方向移动的。
当鼠标是从左右方向移动时,如果x > x0,那么鼠标就是从右边移动的,反之就是从左边移动的;
当鼠标是从上下方向移动时,如果y > y0时,那么鼠标就是从上边移动的,反之就是从下边移动的。
注意:坐标系中所有的y值都是负的。
1 | //这个模块完成鼠标方向判断的功能 |
总结:我觉得第二种方法很简单更能理解,只是在实现起来代码量会更多点。

